Karura
DeFi
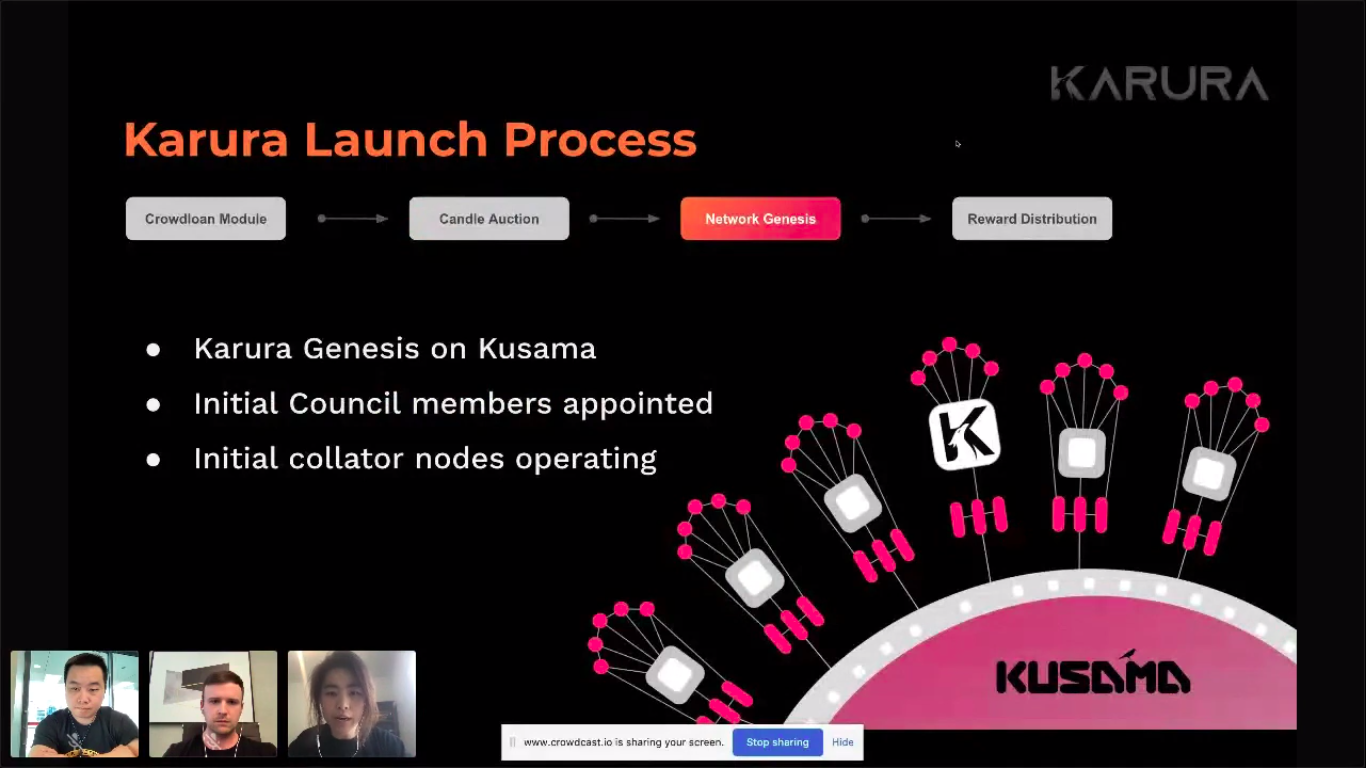
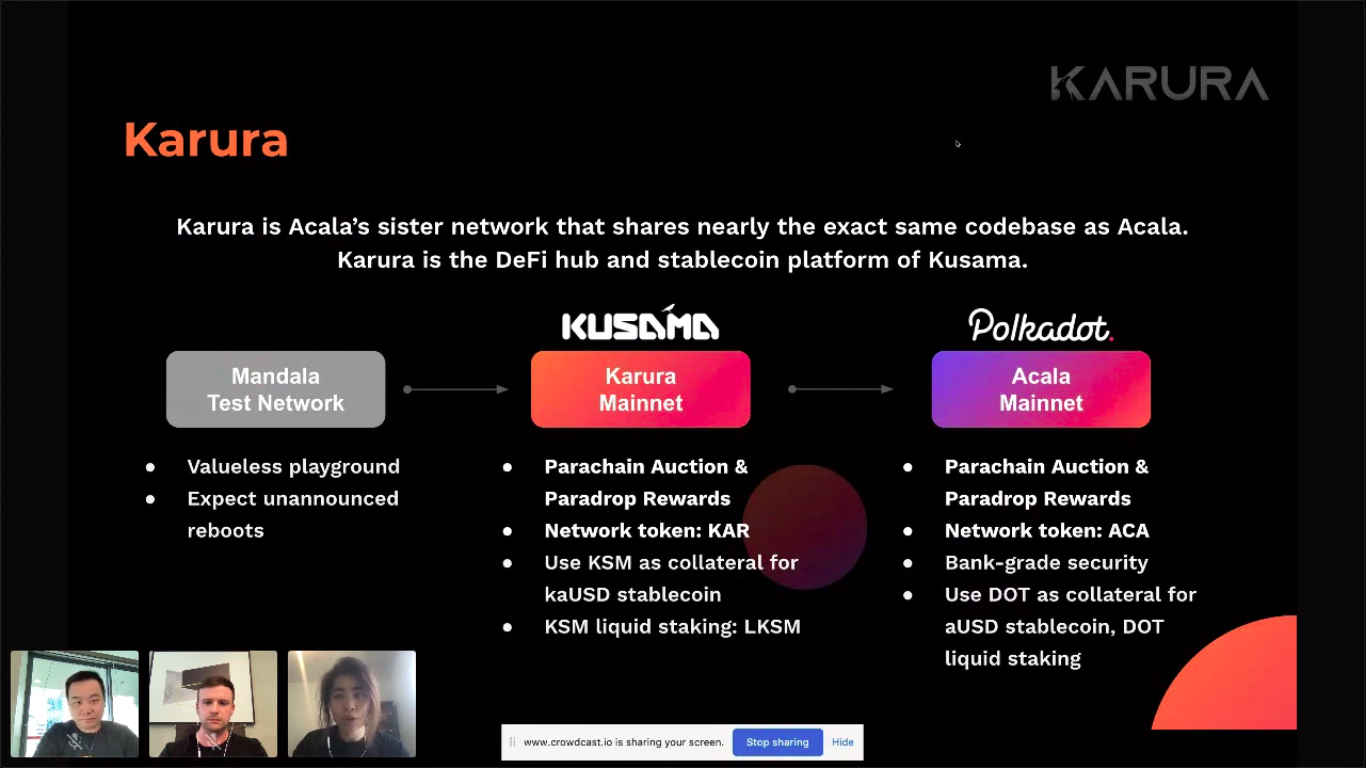
Karura is the all-in-one DeFi hub of Kusama. Founded by the Acala Foundation, Karura is a scalable, EVM-compatible network optimized for DeFi.
The platform offers a suite of financial applications including: a trustless staking derivative (liquid KSM), a multi-collateralized stablecoin backed by cross-chain assets (kUSD), and an AMM DEX – all with micro gas fees that can be paid in any token.
Related Project:
Acala
Acala
Tokens: KAR
W3F Grants:
Links:
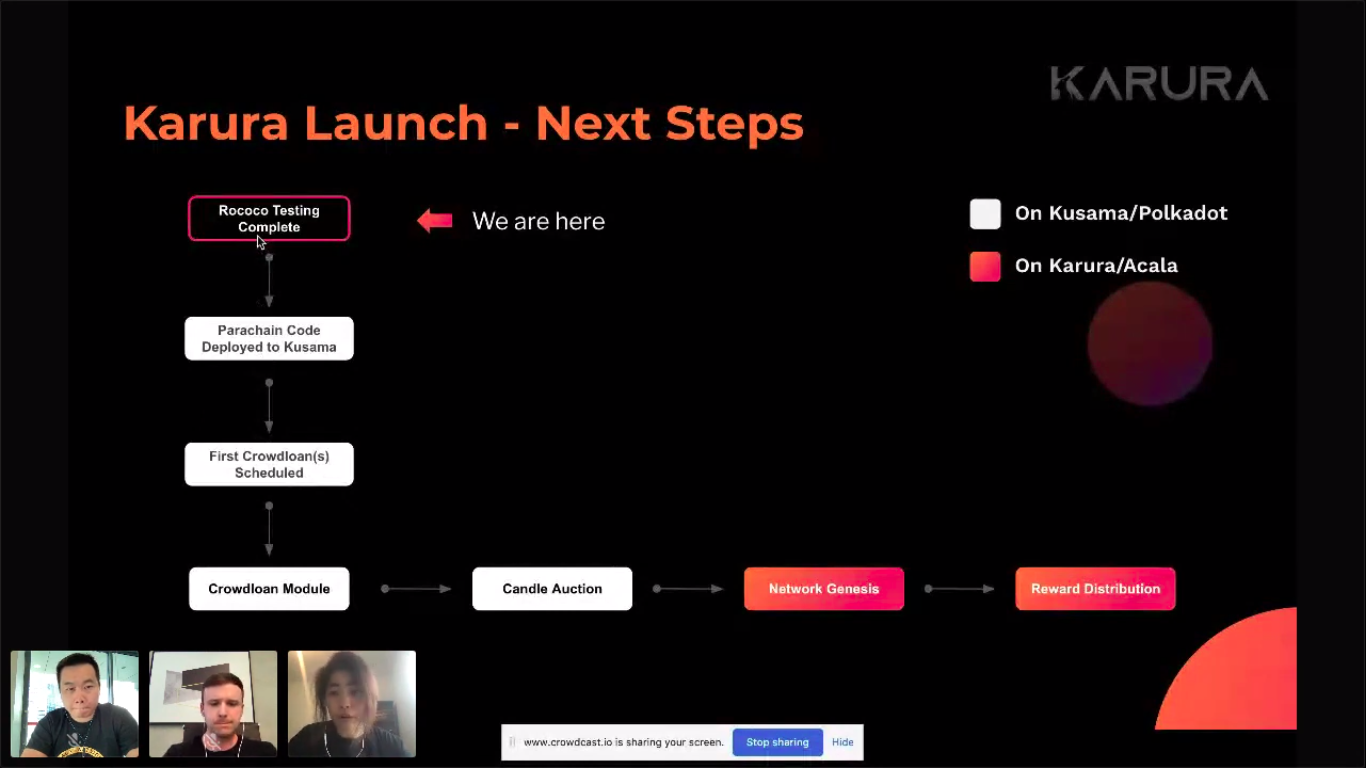
Status
Announced
Testing
Parathread
Kusama
March 24, 2024
February 24, 2025
~34 days remained
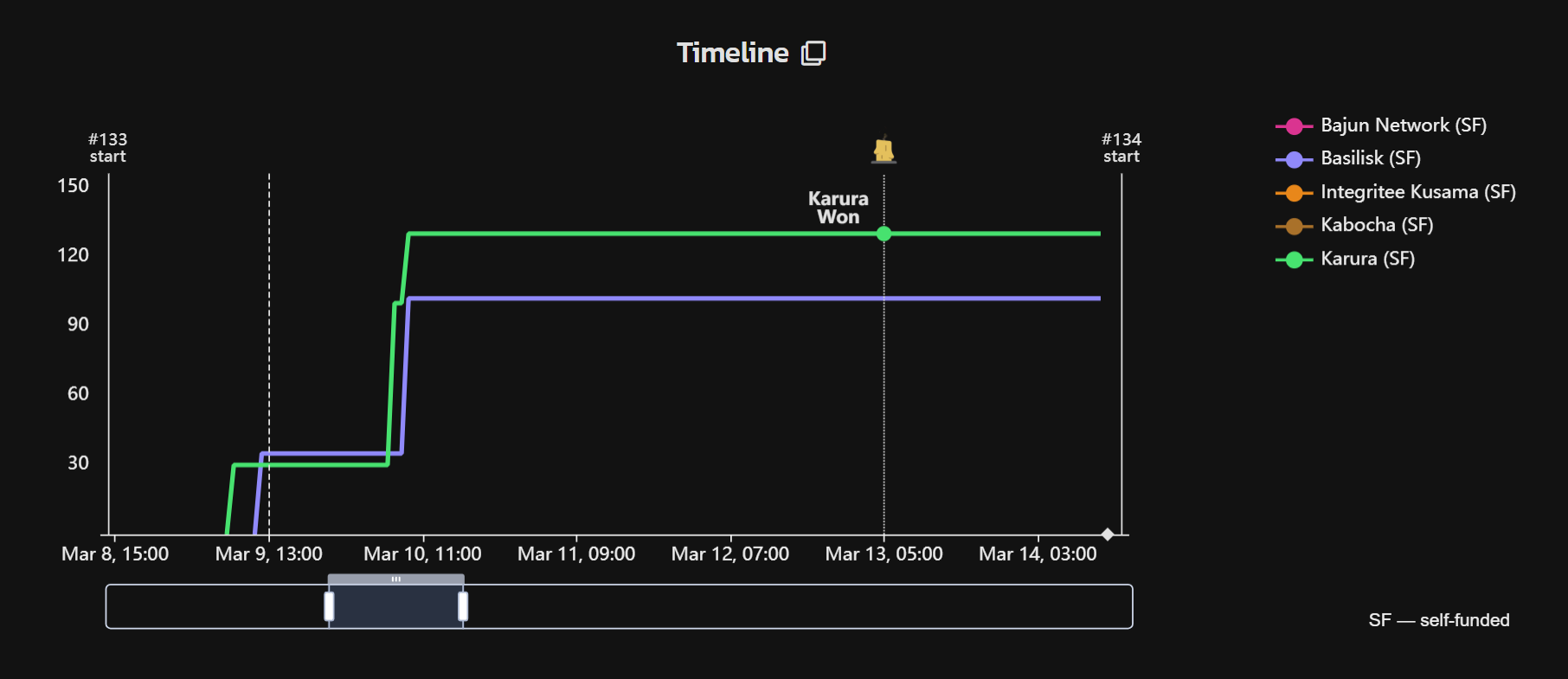
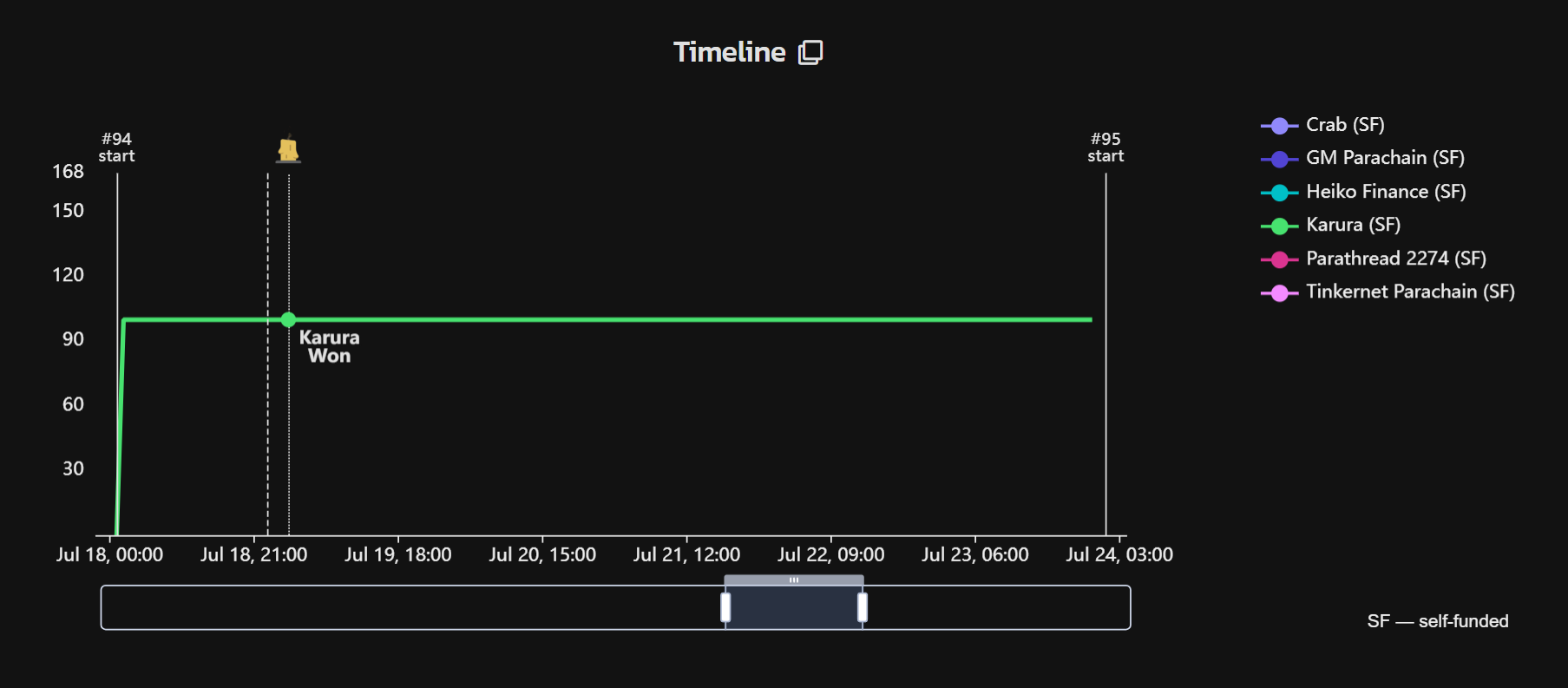
Auction 1: WINNER
Leasing: June 11, 2021 - May 15, 2022
Crowdloan ID:
2000-1
Funds Raised: 501 138 KSM ($13 635 956)
Leading Blocks:
100%
Project Auction Info:
crowdloan details
Reward:
1 KSM :
22+
KAR
Crowdloan Cap: 1 500 000 KSM
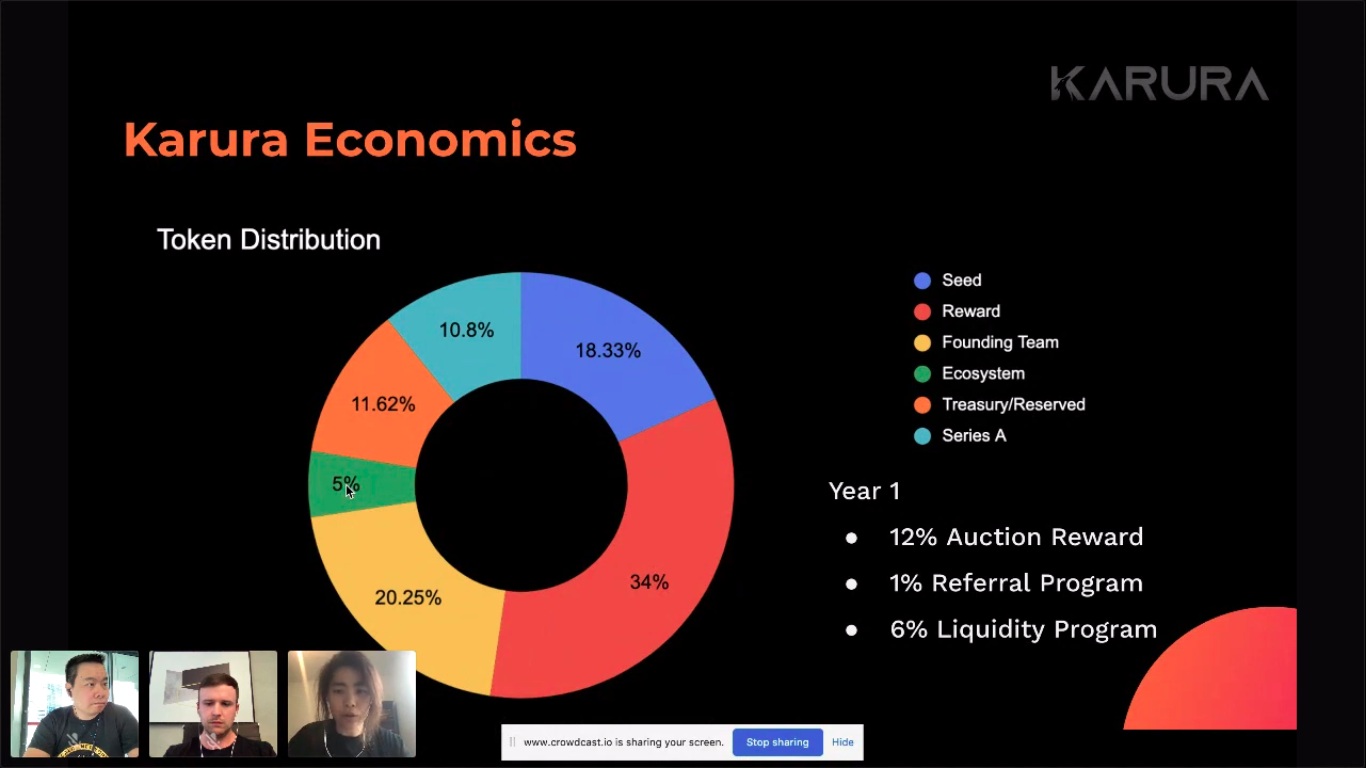
Reward Pool: 11m of 100m (11%)
- 30% KAR will be unlocked, liquid, and available to utilize within Karura’s DeFi
- 70% will be vested and released gradually until the end of the 48-week lease period
.png "Coinbase Ventures")
.png "Altonomy")
.png "Berkeley Blockchain Xcelerator")
Screenshots (12)
Videos (9)
Developer Activity
If you have a connection to this project, kindly Contact Us to keep the details current
Primary Token:
Price:
$0.075
Total Supply:
100 000 000
Circulating Supply:
114 999 994
Market Cap:
$8 646 287
Trading Vol 24:
$201 398
Inflation:
0%
Crowdloan Reward Pool:
11 000 000 (11% of Total Supply)
KAR Distribution
News
Karura is the all-in-one DeFi hub of Kusama. Founded by the Acala Foundation, Karura is a scalable, EVM-compatible network optimized for DeFi.
Slot Acquisition: self-funded
Last Bid: 130 KSM
Leading Blocks: 84.46%
Leasing: March 21, 2024 - February 28, 2025
Karura is the all-in-one DeFi hub of Kusama. Founded by the Acala Foundation. Karura is a scalable, EVM-compatible network optimized for DeFi.
Slot Acquisition: self-funded
Last Bid: 100 KSM
Leading Blocks: 100%
Leasing: July 12, 2023 - June 20, 2024
